Why Kademlia uses XOR as a distance metric
This week, for the distributed systems paper reading accountability group at Recurse Center, I worked through the Kademlia paper: a 2002 paper proposing a distributed hash table variant which is used for applications such as BitTorrent.
Many key advantages of Kademlia hinge on its use of XOR as a distance metric, which is only briefly explained in the paper. I was at first so confused about this, and then, after grokking it, so absolutely tickled with delight that I gave a lightning talk about it and absolutely could not restrain myself from spending my Saturday writing a blog post on how it works.
First, a little Kademlia intuition
Keys are unique random bitstrings gotten by hashing a chunk of data they are henceforth associated with. Node IDs are also unique bitstrings.
Kademlia uses a 160-bit space which is shared by both its keys and node IDs. This is a clever little trick, since any distance function defined over the 160-bit space will now tell us how “close” a node ID is to a key.
XOR = distance
Bitwise intuition
XOR (exclusive OR) is a bitwise function that takes in two bits. This is what its output looks like for all four possible combinations of two 1-bit numbers.
| A | B | XOR(A,B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
In other words, XOR outputs true/high/1 if they are different, or false/low/0 if they are the same. This intuition generalizes when you apply it to N-bit numbers.
If we pick some A==B, or in other words, two N-bit numbers that are as close together as possible because they are the same, then XOR(A,B) will have all low bits.
A = 111...1
B = 111...1
XOR(A,B) = 000...0
On the other hand, if we pick the two numbers such that they are as far away from each other as possible, with all bits being different, then XOR(A,B) will have all high bits.
A = 000...0
B = 111...1
XOR(A,B) = 111...1
So, each individual XOR bit says how “close” A and B are to each other at this particular bit, where low/0 is close, and high/1 is far.
But what’s up when we consider the entire N-bit XOR output as a number? 01000 has the same number of bits flipped as 00001, but 01000 is a lot bigger when we treat it as a number. To answer this, we look at Kademlia’s data structure.
Kademlia’s binary tree structure
Kademlia traverses/queries its bitspace, (or rather, the values associated with its 160-bit keys/ids), using a binary tree of height=160, where the top level of the tree is associated with the head of the 160-bit key, and each successive layer represents the next bit.
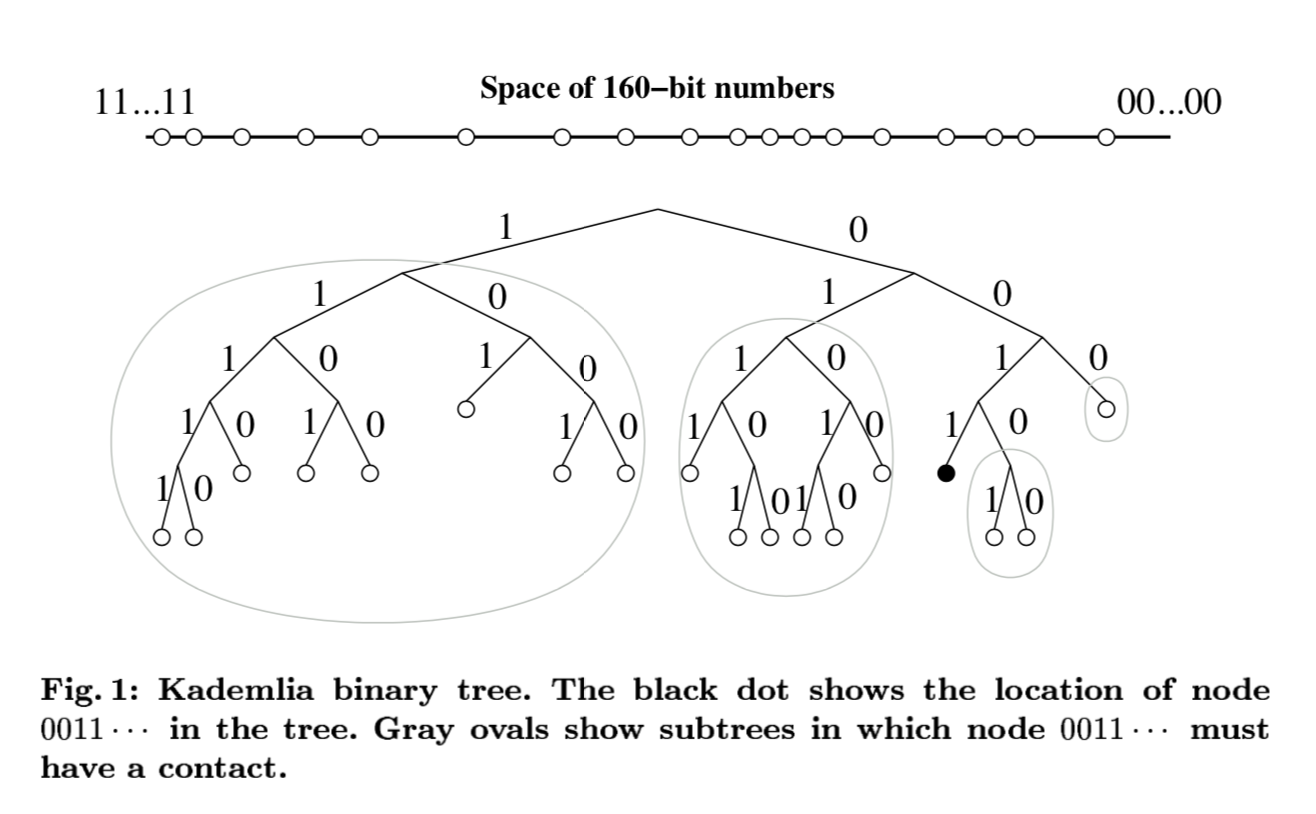
This means that head-end XOR bits, representing the layers higher up in the tree, are a greater contributor to distance. Very reasonable!
A more spatial intuition
Imagine a binary tree like the structure above, but only of height 1, where one branch represents 0 and the other represents 1.
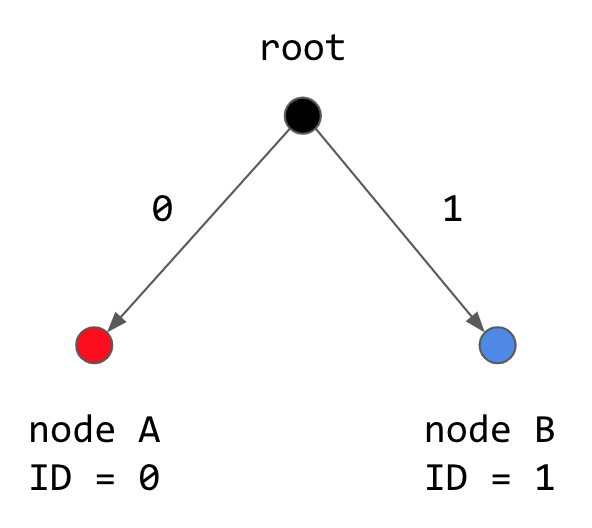
(Nothing has changed, we’re just thinking about XOR in more spatial terms instead of bitwise.)
If the XOR output was 0, there are only two options that could have yielded that result: XOR(0,0) = XOR(1,1) = 0. In other words, both paths either went down the 0 branch together, or down the 1 branch together. XOR=0 is the same as saying that the two paths took the same direction together.
If the XOR output was 1, there are only two options that could have yielded that result: XOR(0,1) = XOR(1,0) = 1. XOR=1 is the same as saying that we took different directions.
Generalize to the larger bitspace, and you see that the XOR of your two 160-bit Kademlia keys expresses where your paths went in the same direction or not.
Benefits of using XOR as a distance metric
What else does XOR tell us?
Note that this is a function of bitwise distance, not of tree edge traversal distance. 00 and 01 are the same number of edge walks away from 11 if you were to trace the tree on paper, but not the same XOR distance.
One super convenient property is that the first high bit in your XOR output between two keys tells you the height of the minimum subtree common to those two keys. In other words, if XOR(A,B) = 0010..., the first high bit is at position 3, meaning that your paths first diverged at the third branch from the root. This property lets Kademlia efficiently leverage subtrees in routing its queries.
Other properties of XOR
XOR is symmetric: the output is the same if you switch the order of the inputs.
XOR is deterministic: the output is always the same when given the same inputs.
This may all sound kind of trivial and obvious in the context of bitwise operations, but it’s extremely valuable in the context of distributed systems. With our weird distance metric deterministically and symmetrically defined across the ID space, no distributed coordination is necessary for nodes in the system to agree that any given pair of keys is the same distance apart, regardless of what state your node has.
This increases Kademlia’s ability to optimize queries. Nodes only need to know about a certain number of other nodes, and can route queries in O(log(n)) steps that get “closer” and “closer” to a given target key.
Pretty cool.